Group representation
Contents
Group representation#
In this section, we will show how symmetry elements can be represented as matrices, and how we can represent their action as simple matrix multiplication, which in turns allow for symmetry operations to be implemented on a computer.
We will use the example of the group of symmetries of a \(n\) vertices regular polyhedron \(D_n\). We can think of this polygon as having vertices on the unit circle, each labeled from \(0\) to \(n-1\).
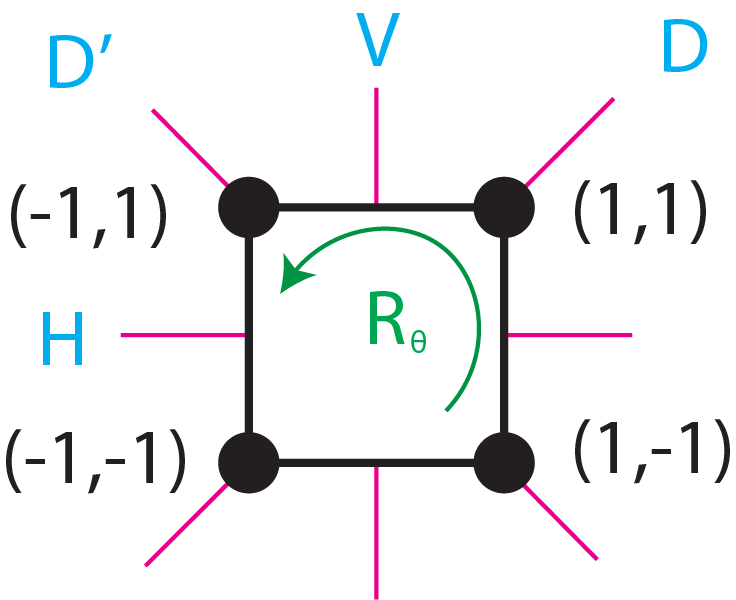
An illustration of a square (4 vertices regular polygon) is presented is Fig. 1. Its set of symmetry element constitute the group element of
where the \(R_{\theta}\) are \(\theta\) counter-clockwise degrees rotations with respect to the center of the square, \(H\) a flips with respect to the horizontal line going through the middle of the upper and bottom edges, \(V\) a flip with respect to the vertical line going through the middle of the left and right edges, \(D\) a flip with respect to the diagonal through the upper right corner and the lower left corner, and \(D'\) a flip with respect to the other diagonal.
|
|---|
Fig.1 - A square and its symmetry elements. |
Representing each vertex by its 2D vector coordinates \(\vec{x}\), the action of a symmetry element \(s \in D_4\) displacement the vertex to its new set of coordinates \(\vec{\hat{x}}\) is defined by the matrix multiplication:
where \(\hat{s}\) is the matrix representation of the symmetry element \(s \in D_4\).
More generally, each rotation can have the following matrix representation:
leading to:
On the other hand, \(H, V , D, D'\) are special cases of reflections about the line through the origin and making an angle of \(\theta\) with the horizontal axis, such that:
and so: